Introduction to Word Embeddings
Word Representation
Word representation
\[
V=[a,aaron,…,zulu,<UNK>]\\
1-hot representation
\]
\[
\eqalign{
\text{Man}\\\text{(5391)}\\
\begin{bmatrix}
0\\0\\0\\0\\ \vdots\\1\\ \vdots\\0\\0
\end{bmatrix}\\
O_{5391}
}
\eqalign{
\text{Woman}\\\text{(9853)}\\
\begin{bmatrix}
0\\0\\0\\0\\0\\ \vdots\\1\\ \vdots\\0
\end{bmatrix}\\
O_{5391}
}
\eqalign{
\text{King}\\\text{(4914)}\\
\begin{bmatrix}
0\\0\\0\\ \vdots\\1\\ \vdots\\0\\0\\0
\end{bmatrix}\\
O_{4914}
}
\eqalign{
\text{Queen}\\\text{(7157)}\\
\begin{bmatrix}
0\\0\\0\\0\\0\\ \vdots\\1\\ \vdots\\0
\end{bmatrix}\\
O_{7157}
}
\eqalign{
\text{Apple}\\\text{(456)}\\
\begin{bmatrix}
0\\ \vdots\\1\\ \vdots\\0\\0\\0\\0\\0
\end{bmatrix}\\
O_{456}
}
\eqalign{
\text{Orange}\\\text{(6257)}\\
\begin{bmatrix}
0\\0\\0\\0\\0\\ \vdots\\1\\ \vdots\\0
\end{bmatrix}\\
O_{6257}
}
\]
I want a glass of orange _____.
I want a glass of apple _____.
Featurized representation: word embedding
| Man (5391) | Woman (9853) | King (4914) | Queen (7157) | Apple (456) | Orange (6257) | |
| Gender | -1 | 1 | -0.95 | 0.97 | 0.00 | 0.01 |
| Royal | 0.01 | 0.02 | 0.93 | 0.95 | -0.01 | 0.00 |
| Age | 0.03 | 0.02 | 0.7 | 0.69 | 0.03 | -0.02 |
| Food | 0.04 | 0.01 | 0.02 | 0.01 | 0.95 | 0.97 |
| \(e_{5391}\) | \(e_{9853}\) |
- The dimension of word vectors is usually smaller than the size of the vocabulary. Most common sizes for word vectors ranges between 50 and 400.
Visualizing word embeddings

- t-SNE
- A non-linear dimensionality reduction technique
- 300 dimensional feature vector or 300 dimensional embedding for each words
- in a two dimensional space so that you can visualize them.
- ex) 300D to 2D
- Word embedding s has been one of the most important ideas in NLP in Natural Language Processing
Using word embeddings
Named entity recognition example
Transfer learning and word embeddings
- Learn word embeddings from large text corpus. (1-100B words) (Or download pre-trained embedding online.)
- Transfer embedding to new task with smaller training set.(say, 100k words)
- Optional: Continue to finetune the word embeddings with new data.
Relation to face encoding(embedding)
\[
\displaylines{
x^{(i)} 👨 \rightarrow \boxed{CNN} \rightarrow \dots \rightarrow \underbrace{\fc}_{f(x^{i})} \rightarrow \\
x^{(j)} 👩 \rightarrow \boxed{CNN} \rightarrow \dots \rightarrow \underbrace{\fc}_{f(x^{j})} \rightarrow
}
\fc \rightarrow \hat y
\]
- encoding and embedding means fairy similar things.
- input any face picture you’ve never seen
- fixed vocabulary like e^{1000}
Properties of word embeddings
Analogies
| Man (5391) | Woman (9853) | King (4914) | Queen (7157) | Apple (456) | Orange (6257) | |
| Gender | -1 | 1 | -0.95 | 0.97 | 0.00 | 0.01 |
| Royal | 0.01 | 0.02 | 0.93 | 0.95 | -0.01 | 0.00 |
| Age | 0.03 | 0.02 | 0.7 | 0.69 | 0.03 | -0.02 |
| Food | 0.04 | 0.01 | 0.02 | 0.01 | 0.95 | 0.97 |
| \(e_{5391}\) | \(e_{9853}\) |
\[
\displaylines{
e_{man}-e_{woman}\approx \begin{bmatrix}-2\\ 0\\ 0\\ 0\end{bmatrix}\\
e_{king}-e_{queen}\approx \begin{bmatrix}-2\\ 0\\ 0\\ 0\end{bmatrix}\\
}
\]
Analogies using word vectors
- in 300D space
- \(e_{man}-e_{woman} \approx e_{king}-e_?\)
- Fill word w: arg max w \( sim(e_w, \underbrace{ e_{king}-e_{man}+e_{woman}}_{30-75\%} ) \)
- t-SNE 300D to 2D
- non-linear mapping
- parallelogram relationship will be broken
Cosine similarity
\( sim(e_w,e_{king}-e_{man}+e_{woman}) \)
\( sim(u,v) = \frac{u^T v}{\|u\|_2 \|v\|_2} \)
Embedding matrix
\[
\overbrace{
\begin{bmatrix}
& & & \color{purple}■ & & & \\
& & & \color{green}■ & & & \\
& & & \color{yellow}■ & & & \\
& & & \color{yellow}■ & E & & \\
& & & \color{yellow}■ & & & \\
& & & \color{yellow}■ & & &
\end{bmatrix}}^\text{a aaron … orange … zulu <UNK>}_{(300,10000)}
\begin{bmatrix}
0\\ 0\\ 0\\ \vdots\\ 1\\ \vdots\\ 0\\
\end{bmatrix}_{(10000,1)}
\]
\[
\displaylines{
E \cdot O_{6257} = \begin{bmatrix}
\color{purple}■\\ \color{green}■\\ \color{yellow}{\displaylines{■\\ ■\\ ■\\ ■}}
\end{bmatrix}_{(300, 1)} = e_{6257}\\
E \cdot O_j = e_j (\text{embedding for word j})
}
\]
\( E \cdot O_j \): It is computationally wasteful.
In practice, use specialized function to look up an embedding.
Learning Word Embeddings: Word2vec & GloVe
Learning word embeddings
Neural language model
I want a glass of orange ____.
\[
\begin{array}{ccc}
I & o_{4343} & \rightarrow & E & \rightarrow & e_{4343}\rightarrow\\
want & o_{9665} & \rightarrow & E & \rightarrow & e_{9665}\rightarrow\\
a & o_{1} & \rightarrow & \color{yellow}E & \rightarrow & e_{1}\rightarrow\\
glass & o_{3852} & \rightarrow & \color{yellow}E & \rightarrow &e_{3852}\rightarrow\\
of & o_{6163} & \rightarrow & \color{yellow}E & \rightarrow &e_{6163}\rightarrow\\
orange & o_{6257} & \rightarrow & \color{yellow}E & \rightarrow & \underbrace{e_{6257}}_{\cancel{1800}\color{yellow}1200}\rightarrow\\
\end{array}
\underbrace{\fc}_{\uparrow w^{[1]}, b^{[1]}} \rightarrow \underbrace{\circ}_{\text{softmax} \leftarrow w^{[2]},b^{[2]}}
\]
- Input 1800 dimensional vector obtained by taking 6 embedding vectors and stacking together.
- fixed history: just look previous 4 words (hyperparameter of the algorithm)
- that network will input a 1200 dimensional feature vector.
- paper
Other context/target pairs
I want a glass of orange juice to go along with my cereal.
- Context: Last 4 words.
- 4 words on left & right
- a glass of orange ? to go along with
- Last 1 word
- orange ?
- Nearby 1 word
- glass ?
- skip-gram
- 4 words on left & right
Word2Vec
Skip-gram
I want a glass of orange juice to get along with my cereal.
- window: +-10 words
- Context: orange
- Target : juice, glass my… randomly chose
- paper
Model
\[
\displaylines{
\text{Vocab size}=10,000k\\
Content: c (“orange”) \rightarrow Target: t (“juice”)\\
o_c \rightarrow E \rightarrow e_c \rightarrow \circ(softmax) \rightarrow \hat y\\
\text{softmax}: p(t|c)=\frac{e^{\theta_t^T e_c}}{\sum_{j=1}^{10,000} e^{\theta_j^T e_c}}\\
\theta_t: \text{parameter associated with output} t\\
\mathfrak{L}(\hat y, y)=-\sum_{i=1}^{10,000} y_i log \hat y_i\\
y=\begin{bmatrix}
0\\\vdots\\1\\\vdots\\0
\end{bmatrix}
}
\]
Problems with softmax classification
\[
\displaylines{
p(t|c)=\frac{e^{\theta_t^T e_c}}{\sum_{j=1}^{10,000} e^{\theta_j^T e_c}}\\
}
\]
- How to sample the context c?
- extremely frequently: the, of, a, and, to…
- don’t appear often: orange, apple, durian…
Negative Sampling
Defining a new learning problem
I want a glass of orange juice to go along with my cereal.
| x | x | y |
| Context | word | target? |
| orange | juice | 1 |
| orange | king | 0 |
| orange | book | 0 |
| orange | the | 0 |
| orange | of | 0 |
k=4 (king, book, the, of)
- Choose k:
- k=5~20: smaller dataset
- k=2~5: larger dataset
- paper
Model
\[
\text{softmax}: p(t|c)=\frac{e^{\theta_t^T e_c}}{\sum_{j=1}^{10,000} e^{\theta_j^T e_c}}\\
P(y=1|c,t)=\gamma(\theta_t^T e_c)\\
\]
- before: 10,000 softmax problem
- now: 10,000 binary classification problem
Selecting negative examples
| x | x | y |
| Context | word | target? |
| orange | juice | 1 |
| orange | king | 0 |
| orange | book | 0 |
| orange | the | 0 |
| orange | of | 0 |
t → king, book, the, of
\[
P(w_i)=\frac{f(w_i)^{\frac34}}{\sum_{j=1}^{10,000} f(w_i)^{\frac34}}
\]
- 3/4
- heuristic value
- Mikolov did was sampled proportional to their frequency of the word to the power 3/4
- from whatever’s the observed distribution in English text to the uniform distribution.
- if you run the algorithm
- use open source implementation
- use pre-trained word vectors
GloVe word vectors
GloVe (global vectors for word representation)
I want a glass of orange juice to go along with my cereal.
\( X_{ij}=X_{tc}=\text{ times } j \text{ appears in context of } i \)
- depending on the definition of context and target words
- \(X_{ij}=X_{ji}\)
- c and t whether or not appear within +- 10 words each other
- symmetric relationship
- always the word immediately before the target word
- not be symmetric
- \(X_{ij}\) is a count that captures how often do words i and j appear with each other, or close to each other.
- paper
Model
\[\text{minimize} \sum_{i=1}^{10,000}\sum_{j=1}^{10,000} \underbrace{f(X_{ij})}_{\text{weighting term}}(\theta_i^T e_j + b_i + b’_j -\log X_{ij})^2
\]
- weighting term
- heuristics for choosing this weighting function F
- \( X_{ij}\rightarrow 0, \log X_{ij} \rightarrow \infty \)
- less frequent words: more weight
- more frequent words: little weight
- \( f(0)=0 \): The weighting function helps prevent learning only from extremely common word pairs. It is not necessary that it satisfies this function.
- \(\theta, e\)
- roles of theta and e are now completely symmetric
- \(\theta_i, e_j\): symmetric
- initialize \(\theta\) and \(e\), uniformly random and gradient descent to minimize every word then take the average.
- \( e_w^{final}=\frac{e_w+\theta_w}{2}\)
A note on the featurization view of word embeddings
\[
\displaylines{
\text{minimize} \sum_{i=1}^{10,000}\sum_{j=1}^{10,000} f(X_{ij})({\color{blue} \theta_i^T e_j} + b_i + b’_j -\log X_{ij})^2\\
(A\theta_i)^T(A^{-T}e_j)=\theta_i \cancel{A^T A^{-T}} e_j
}
\]
- features easily humanly interpretable axis
- features might be combination of gender,royal,age ,and food and all the other features
- arbitrary linear transformation of the features, you end up learning the parallelogram平行四辺形 map for figure analogies still works.
Applications using Word Embeddings
Sentiment Classification
Sentiment classification problem
| x | y |
| The dessert is excellent | ★★★★☆ |
| Service was quite slow | ★★☆☆☆ |
| Good for a quick meal, but nothing special | ★★★☆☆ |
| Completely lacking in good taste, good service, and good ambience. | ★☆☆☆☆ |
- not have a huge label data set.
- 10,000-100,000 words would not be uncommon
Simple sentiment classification model
The dessert is excellent. ★★★★☆
\[
\begin{array}{ccc}
The & o_{8928} & \rightarrow & E & \rightarrow & e_{8928}\rightarrow\\
dessert & o_{2468} & \rightarrow & E & \rightarrow & e_{2468}\rightarrow\\
is & o_{4694} & \rightarrow & E & \rightarrow & e_{4694}\rightarrow\\
excellent & o_{3180} & \rightarrow & \underbrace{E}_{\uparrow 100B} & \rightarrow &e_{3180}\rightarrow
\end{array}
\underbrace{\text{Avg.}}_{\uparrow 3000} \rightarrow \underbrace{\circ}_{\text{softmax} \leftarrow ★} \rightarrow \hat y
\]
- So notice that by using the average operation here, this particular algorithm works for reviews that are short or long text.
- Very negative review problem
- Completely lacking in good taste, good service, and good ambience.
RNN for sentiment classification
- it will be much better at taking word sequence
- word embeddings can be trained from a much larger data set, this will do a better job generalizing to maybe even new words now that you’ll see in your training set.
Debiasing word embeddings
The problem of bias in word embeddings
Man:Woman as King:Queen
Man:Computer_programmer as Woman:Homemaker (bad)
Father:Doctor as Mother:Nurse (bad)
Word embeddings can reflect gender, ethnicity, age, sexual orientation, and other biases of the text used to train the model.
Addressing bias in word embeddings
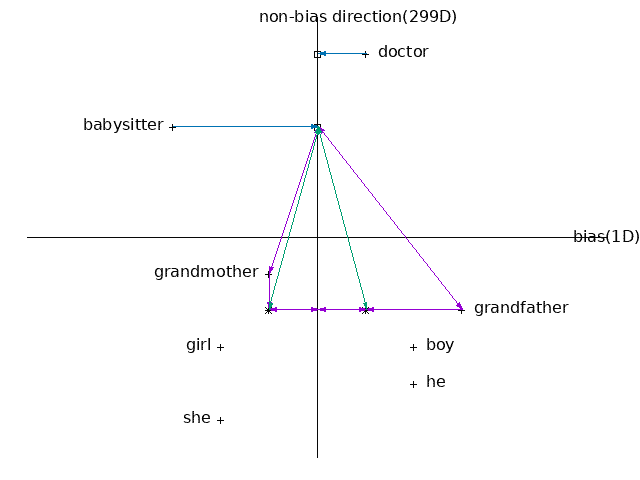
- 1. Identify bias direction.
- \( e_{he}-e_{she}\)
- \( e_{male}-e_{female}\)
- ↑average
- 2. Neutralize: For every word that is not definitional, project to get rid of bias.
- 3. Equalize pairs.
- grandmother – grandfather
- similarity, between babysitter and grandmother is actually smaller than the distance between babysitter and grandfather.
- maybe reinforces an unhealthy, or maybe undesirable, bias that grandmothers end up babysitting more than grandfathers.
- girl – boy…
- grandmother – grandfather
- So the final
- how do you decide what word to neutralize?
- beard
- what words should be gender-specific and what words should not be.
- most words in the English language are not definitional, meaning that gender is not part of the definition.
- how do you decide what word to neutralize?
- paper
Programming assignments
Operations on word vectors – Debiasing
After this assignment you will be able to:
- Load pre-trained word vectors, and measure similarity using cosine similarity
- Use word embeddings to solve word analogy problems such as Man is to Woman as King is to __.
- Modify word embeddings to reduce their gender bias
Emojify
Using word vectors to improve emoji lookups
- In many emoji interfaces, you need to remember that ❤️ is the “heart” symbol rather than the “love” symbol.
- In other words, you’ll have to remember to type “heart” to find the desired emoji, and typing “love” won’t bring up that symbol.
- We can make a more flexible emoji interface by using word vectors!
- When using word vectors, you’ll see that even if your training set explicitly relates only a few words to a particular emoji, your algorithm will be able to generalize and associate additional words in the test set to the same emoji.
- This works even if those additional words don’t even appear in the training set.
- This allows you to build an accurate classifier mapping from sentences to emojis, even using a small training set.
What you’ll build
- In this exercise, you’ll start with a baseline model (Emojifier-V1) using word embeddings.
- Then you will build a more sophisticated model (Emojifier-V2) that further incorporates an LSTM.